|
ゲームに戻る
バックギャモン初期配置とゲームの目的バックギャモンがBrainKingの他のボードゲームと大きく違う点は通常のボードゲームは真四角の盤上で行われるのに対し、このゲームはアイスクリームのコーンのような三角形の形をした枠が上下にある特殊な形のボードを使う点です。また、このゲームはポーカー同様、サイコロの目によって動きが決定するという点も他のゲームとは決定的に違います。 バックギャモンには合計24の三角のマスがありますがそのうち19から24までのマスを白の陣地、1から6までのマスを黒の陣地と呼びます。各プレーヤーは以下の図にあるように15個の丸い駒を使ってゲームを開始します。  このゲームの目的は味方の駒を全て上がらせ、敵側が先に上がることを阻止することです。片方のプレーヤーの駒が全て上がった状態のときにゲームが終了します。 駒の動き プレーヤーは自分の番になったらサイコロを振り、サイコロの目に従って一つかそれ以上の駒を動かします。サイコロはプレーヤーがページを最初に開いたときに自動的に振られます。1回サイコロが振られるとその手に使うサイコロの目の数はページを更新しても変わりません。現在手のサイコロの目は盤の右半分に(大きなサイコロ)、敵の前の手のサイコロの目は盤の左半分に小さなサイコロとして表示されます。2つのサイコロの目が違う数字がでた場合2手分動かすことができます。まず、左隅のサイコロの目の数分だけ一つの駒を動かし、今度は右のサイコロの数の分だけ駒を動かします。2手の動きには同じ駒でも違う駒でも使用できます。 2つのサイコロロの目が同じの場合、4手分動かすことができます。例えば両方のサイコロが5の目が出た場合、5マス分の動きを4回行うことができます。白のプレーヤーは駒を逆時計回りに(1から24まで)、黒のプレーヤーは駒を時計回りに動かします。以下の図は白と黒の駒が動く前と後を示しています。 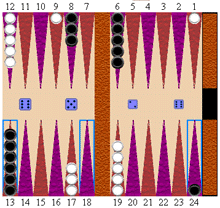  上の図では白は一つの駒を9から15まで六マス動かし、もう一つの駒を1から4まで3マス分動かしています。  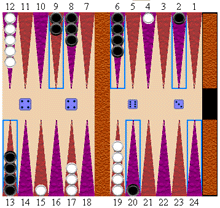 上の図は黒が24から20まで、13から9まで、13から9まで、6から2まで四つの駒を4マス動かしたところです。 敵の駒の取り方 プレーヤーが敵の駒を取れるのは、三角マスの中に敵の駒が一つしかないときだけです。この状態のことを ブロット と呼びます。取った駒は盤から取り除かれるとバーと呼ばれている場所に置かれます。以下の図は白が17から20まで動いて黒の駒を取ったところです。 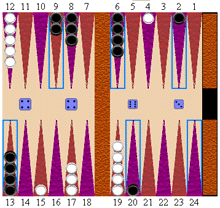  自陣の駒を全てあがらせる方法 プレーヤーは以下の条件がそろったときに自分の駒を全て上がらせることができます。
その他の重要なルール
ダブリングキューブ バックギャモンおよびその変則ゲームにおいてはダブリングキューブと呼ばれる独特のルールがあります。バックギャモンの競技においては一定の目標点数をあらかじめ設定し、そのポイントまでは早く到達したプレーヤーが勝ちとなります。1回のゲーム(一試合は何回かのゲームによって構成される)での獲得点数は得点計算のルールおよびダブリングキューブで出た値によっても大きく異なりますが詳しくは以下の段で説明します。 キューブはゲーム盤の右端に表示され、最初の数値は1に設定されています。  ゲームにおいてダブリングキューブを使う場合、各プレーヤーはサイコロを振って通常の動きを行うか、ダブルを行うかを選択します。ダブルを申し込まれた場合、相手方はダブルを受けるか断るかを選択しなければなりません。ダブルを受け入れるたびにダブリングキューブの値は倍となっていきます。ダブルの申し出を断った場合現在のゲームは敗北扱いとなり勝者にダブリングキューブの値が加算されます。ギャモン、バックギャモンはダブルの申し出が断られたときには適用されません。 (得点の項を参照)。 ダブルの申し出が受諾されると、今度はダブルを受けた側にダブル行使の選択肢が与えられ、キューブの値は前の数字の倍の値が表示されます。次の図は第1回目のダブルが受け入れられた状態を示しています。: 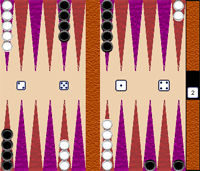 ダブリングキューブの値は4、8、16、32、64とダブルが行われるたびに倍になっていきます。最初にダブルが受け入れられると、この次にダブルの申し出ができるのはキューブの所有者のみです。つまり双方のプレーヤーが交互にダブルの申し出を出し合うことになるのです。 得点 片方のプレーヤーが全ての駒を上がらせたときに一ゲームは終了となり相手の駒の位置によりそれに応じた得点が勝ったプレーヤーに加算されます。
勝ち点にさらにダブリングキューブの倍率を掛けます。例えばキューブの値が4でバックギャモン勝ちを収めた場合、4x3=12点の得点が加算されます。 その他の重要なダブリングキューブのルール
このゲームに参加する 参照: バックギャモン, ナックギャモン, 逆バックギャモン, バックギャモン競争, 混みバックギャモン, ハイパーバックギャモン, クローン・バックギャモン, キリギリス・バックギャモン, プラコト, フェヴガ |
日時
オンライン友達
気に入り掲示板
同好会
今日のアドバイス
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
著作権 © 2002 - 2025 Filip Rachunek. 上へ |























